In this post we will take a brief look at Ghidra, a tool developed by the NSA for the reversing. Ghidra is a powerful program with a lot of options, and we will be exploring them in different tutorials by resolving different reversing challenges. In this tutorial we will look at the installation, project creation and overview by resolving a simple crackme.
Installation
To run Ghidra, you need to install JDK 11 64-bit. Afterwards, you can find the releases you need to download here and extract it. Then, simply run it with:
./ghidraRun
or
ghidraRun.bat
On Windows
Simple reversing
For this example we will get a binary from the website Crackmes.one. It is a very simple example that will allow us to introduce to Ghidra.
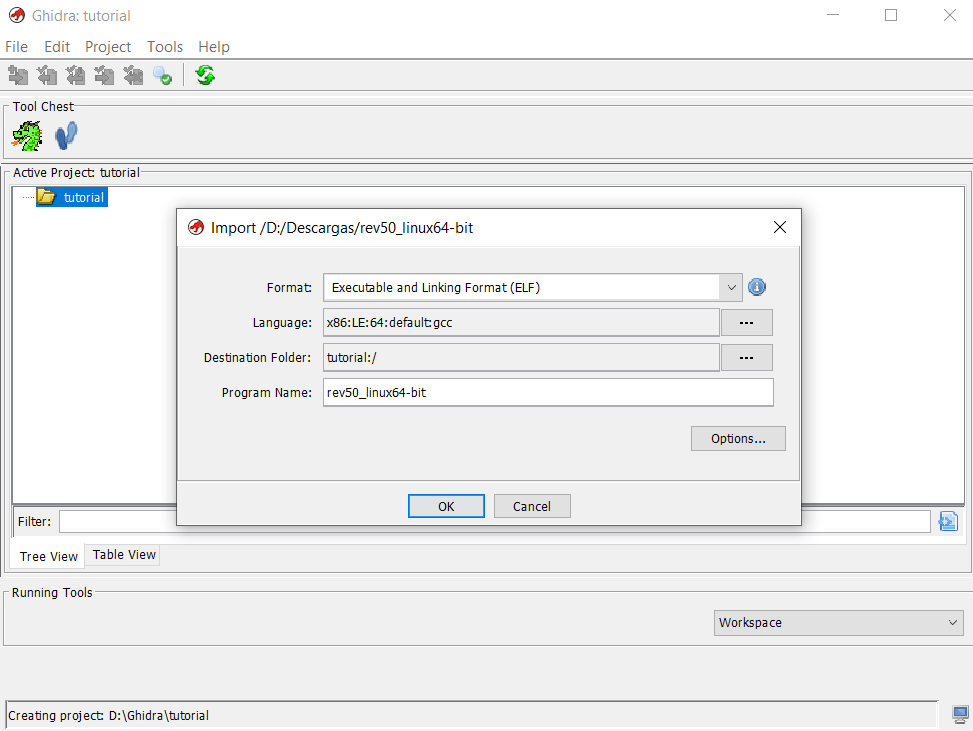
We first create a new project under “File -> New Project”. Then, once the project is created, we go to File-> Import File and select the crackme we downloaded. The first window we will se is something like this:
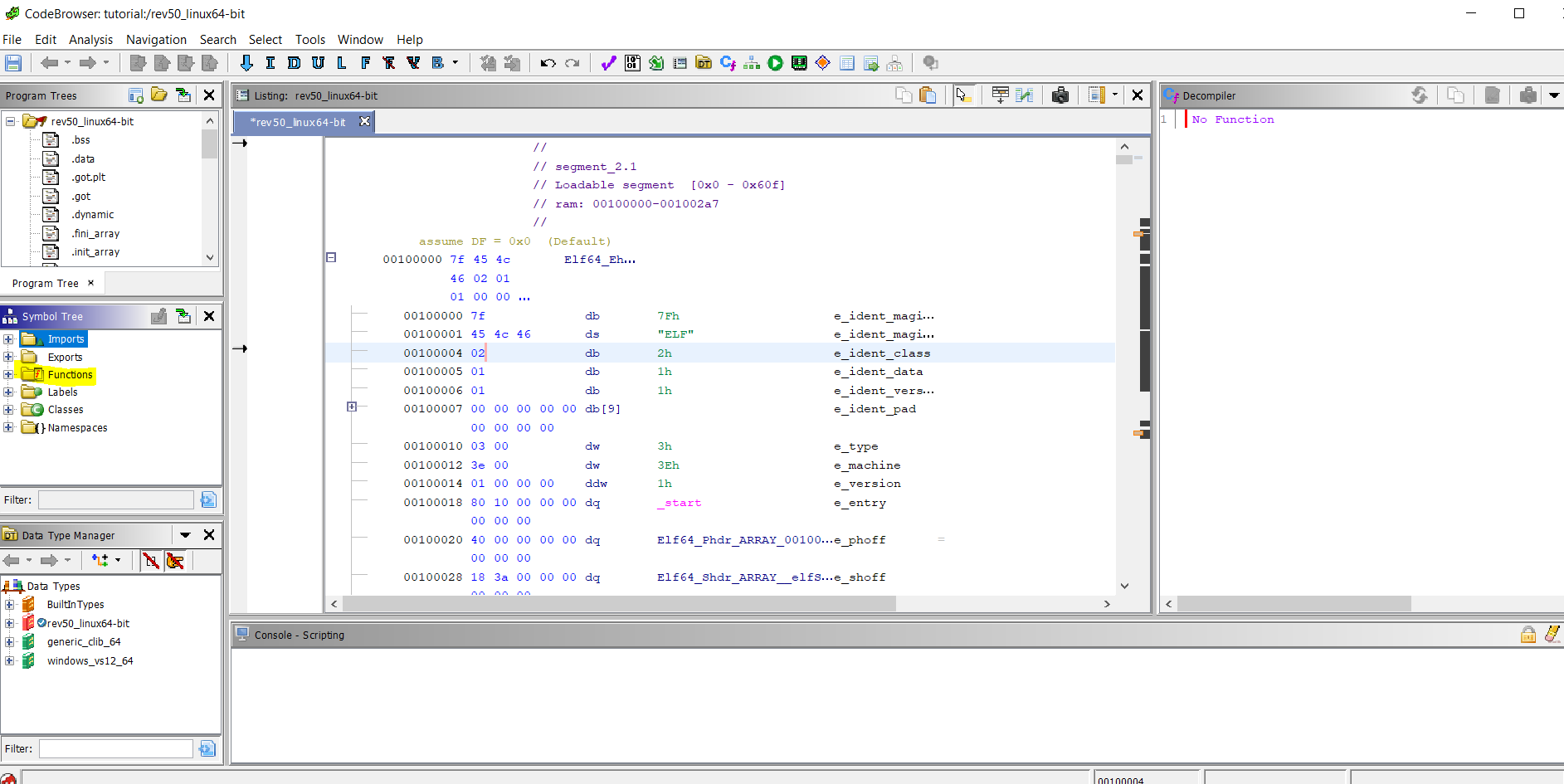
We can see that Ghidra detected the language automatically. Afterwards, it shows us a summary of the results. We can now start the CodeBrowser by double-clicking the file and it will asks us if we want to analyse the binary and will show us a lot of options. We can leave it by default for now, and click analyze. We will see the disassembly:
We can start by looking at the Symbol Tree, and expanding the functions node. We can see that all the functions of the program are there. If we click in one, we can see the C code in the Decompiler window. If we click the main function, we will see this:
If we take a look at the code, we notice that param_1 is the number of inputs (argv) and param_2 is our input (argc). We can see that the program is storing in sVar1 the lenght of our input and comparing it with 10. If it is 10, it will check that the 5th position is equal to @. So any 10 character string whose 5th position is @ will be a valid password:
Nice Job!!
flag{1111@11111}
In the following posts about Ghidra we will take a deeper look at Ghidra functions by solving more challenges.